Application Research of CDKF Filtering Algorithm in GPS Integrated Navigation System
1 Introduction
This article refers to the address: http://
The Global Positioning System (GPS) is widely used in vehicle positioning because it provides all-weather, continuous, real-time, high-precision positioning information. However, when the vehicle is driving in a special geographical environment such as an underground tunnel or a high-rise building, the GPS satellite occlusion problem may cause the GPS to be unable to be normally positioned. Based on this, the general vehicle navigation system generally adopts a low-cost dead reckoning system (DR) and GPS. To form a combined positioning system. When the GPS signal is lost and cannot be located, the DR system can continue to work and the reliability of the system is improved [1-2].
The actual vehicle integrated navigation system model is generally non-linear. Using the extended Kalman filter (EKF) method, the linear equation is linearly truncated around the state estimation and the first-order linearization truncation is performed. The linearized standard Kalman filter model of the system can be established. However, in practical applications, EKF also has some shortcomings: if the high-order term in the Talor expansion of the nonlinear observation equation cannot be ignored, EKF will cause a large linearization error, making the filter difficult to stabilize [3- 4].
In response to the deficiencies of EKF, a new set of nonlinear filtering methods, Sigma-Point Kalman Filter (SPKF), has been used in recent years, which uses weighted statistical linear regression (WSLR) to pass a set of deterministic sampling points ( Sigma point) to capture the relevant statistical parameters of the system. According to the Sigma point selection, it is mainly divided into Unscented Kalman Filter (UKF) and Center Differential Kalman Filter (CDKF) [5].
The advantage of the CDKF filtering algorithm is that it overcomes the shortcomings of the EKF method. It does not require a specific analytical form of the system model for filtering, and fully considers the noise statistical characteristics of random variables, with less linearization error and higher positioning than EKF. Precision, which is much less sensitive to state covariance and faster approaching UKF. The study found that another advantage of CDKF is that only one parameter h is used, which is easier to implement in practical applications than the UKF that needs to determine three parameters [6].
In this paper, the GPS/DR integrated navigation system is filtered by CDKF, UKF and EKF. The experimental results further show that the CDKF method is superior to the EKF and UKF methods, which is a more ideal nonlinearity in vehicle integrated navigation. The filtering method truly realizes the low-cost, high-precision real-time positioning of the vehicle.
2 Center Differential Kalman Filter (CDKF) algorithm description
The starting point of CDKF is to use the sterling interpolation formula to approximate the derivative of the nonlinear equation with a polynomial, thus avoiding complex derivation operations. It uses the center difference instead of the first and second derivatives in the Talor expansion [7]. For the L-dimensional state vector, the number of sigma points of CDKF is 2L+1. In order to make the sigma point have the same mean, variance and high-order center moment as the true state distribution, the sigma point and the weight are constructed according to (1):

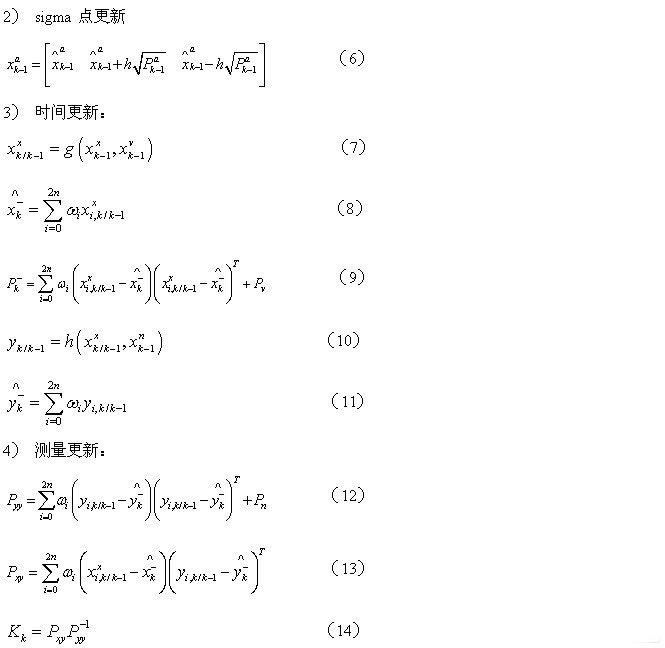

3 test plan design and implementation
In order to verify the effectiveness and superiority of the new Kalman filter described in this paper, two GPS receiving platforms with different precisions are used. The high-precision GPS receiving platform uses the receiver with higher precision and DGPS method. High-precision dynamic positioning data as the true value of the system. The low-precision GPS receiving platform selects the receiver with a precision different from the former and the single-machine GPS method. The received low-precision dynamic positioning data is used as the filtering object of the Kalman filter, and the state estimation value and the system state real value after filtering are used. Compare to measure the effect of the filter.
3.1 Test platform and software
The high-precision GPS receiving platform here uses CMC AllStar Base GPS board and MDS company MDS OEM Series TM radio as the base station. The mobile station selects CMC SuperStar GPS board and MDS company MDS OEM Series TM radio station to keep the positioning accuracy at the same time. 2m or so. The low-precision GPS receiving platform uses the OEM board GPS35LP (GPS35-HVS) from GARMIN. In February 2008, the author set up the DGPS base station in the electrical building of Jiangsu University. The DGPS mobile station and the stand-alone GPS receiver were placed in the car, and the uniform motion was carried out at the entrance of the Jiangsu University School. The starview monitor and u-center were used. 4.01 synchronous reception of data on the host computer. The test equipment is shown in Figure 1 and Figure 2.

Figure 1 DGPS base station

Figure 2 DGPS mobile station and stand-alone GPS
3.2 Test results and analysis
Part of the data received by the test is as follows: See Table 1.
Table 1 Received data from the receiver

The new CDKF filtering algorithm is applied to the GPS navigation and positioning system. The EKF, UKF and CDKF filtering algorithms are used to filter the GPS data obtained by the experiment. The test results are shown in Figures 3 and 4. In order to more intuitively express the effects of the three filtering algorithms, the error mean values ​​of the three filtering methods are listed in Table 2.

It can be seen from the filtering curve Fig. 3 and Fig. 4 that the northeast direction position error using CDKF and UKF filtering is controlled within 10 meters, and the position error using EKF is relatively large; from Table 2, it can be concluded that the mean value of the latitude and longitude error Compared with the northeast speed error, the CDKF and UKF algorithms are also significantly better than the EKF. It can be seen that the positioning accuracy and reliability of the CDKF filter are much higher than those of the EKF, but the calculation of the UKF is slightly higher than that of the EKF. The calculation parameters of CDKF relative to UKF are reduced, so the approach speed is relatively increased, and the calculation amount is also reduced.
Table 2 Error comparison of three filtering algorithms

4 Conclusion
In this paper, a new filtering algorithm-center differential Kalman filter is described and applied to the GPS/DR integrated navigation system. The obvious advantages in the filtering method and calculation process are analyzed. The parameters are debugged through multiple experiments. The experimental comparison of EKF, UKF and CDKF filters is obtained. CDKF is superior to the former two in terms of positioning accuracy and speed, and its implementation is relatively simple, and its application range is wider. It is a dynamic system. An effective state estimation algorithm.
references
[1] Fu Mengyin, Deng Zhihong, Zhang Jiwei. Kalman filtering theory and its application in navigation system [M]. Beijing: Science Press, 2003.
[2] Liu Yang, Pan Xiaogang, Wang Zhengming, Yi Dongyun. Adaptive UKF real-time inter-satellite relative positioning method based on enhanced GPS[J]. Journal of Surveying and Mapping, 2008,(01)
[3] Zhang Chuanbin, Tian Weifeng, Jin Zhihua. UKF Filtering Method and Its Application in Vehicle Navigation State Estimation[J]. Journal of System Simulation, 2005, 17(6): 1456-1458.
[4] R. van der Merwe. "Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models". PhD thesis, OGI School of Science & Engineering at Oregon Health & Science Universit, Portland, OR, April 2004.
[5] Kazufum i Ito and KaiqiXiong. Gaussian Filters for Nonlinear Filtering Problems [J]. IEEE Transactions on Automatic Control, may2000, 45(5): 910-927.
[6] Tom V, Wang Xiaodong. Decentralized Sigma-Point Information Filters for Target Tracking in Collaborative Sensor Networks . IEEE Transactions on Signal Processing, 2005, 53 (8) : 2997-3009 .
[7] Liu Guohai, Li Kangji. Method for improving GPS positioning accuracy based on PDA[J]. Journal of Jiangsu University: Natural Science Edition, 2005, 26(5): 448-452. LIU Guo-hai, Li Kang-ji. GPS positioning accuracy based on PDA [J]. Journal of Jiangsu University: Natural Science Edition, 2005, 26(5): 448-452. (in Chinese)
Rotor Core,Copper Rotors,Copper Rotors With Shafts,Rotor Assembly
Henan Yongrong Power Co., Ltd , https://www.hnyongrongglobal.com