Research on Fuzzy Control of Double Inverted Pendulum
Research on Fuzzy Control of Double Inverted Pendulum
1 Introduction
In the development of control theory, the correctness of a certain theory and the feasibility of practical application all need a controller designed according to its theory to control a typical object for verification. The inverted pendulum is such a controlled object. The inverted pendulum system is a multivariable, fast, nonlinear and naturally unstable system. During the control process, the system can effectively reflect many key problems in the control, such as nonlinear problems, system robustness problems, follow-up problems, Calm the problem and track the problem. Inverted pendulum is an ideal experimental device in the research of control theory. The control goal of the inverted pendulum system of the trolley is that the inverted pendulum can be stabilized on the guide rail of a limited length without falling down by the trolley, thereby achieving dynamic balance. This paper aims at the nonlinear model of the double inverted pendulum. Based on the Maminadi model, the fuzzy controller is designed by designing the fusion function to effectively solve the rule explosion problem and realize the effective control of the double inverted pendulum.
2 Establishment of mathematical model of double inverted pendulum
The second-level inverted pendulum is composed of a trolley, a swing rod, a horizontal guide rail, etc. The trolley is driven by a servo motor, a pulley, and a transmission belt to move left and right on the horizontal guide rail. The trolley and the upper and lower swing rods are connected by bearings, and a potentiometer is fixed at each bearing connection to detect the angular deviation of the two swing rods from the vertical line. The offset position of the trolley relative to the center point of the track is also detected by a potentiometer fixed on the pulley shaft.
The basic principle is: after the angle and position signals are acquired by the detection circuit, the corresponding differential signals are obtained by the differential circuit, and these signals are converted into digital signals by the A / D converter and transmitted to the computer. Calculate the required voltage value of the control force through the designed control program, convert it into an analog signal through the D / A converter, drive the motor to run after power amplification, and then use the belt to drag the trolley to reciprocate on the guide rail to realize the effective of the inverted pendulum control. Ignore air resistance and various frictions, and consider the pendulum as a rigid body. Figure 1 is a schematic diagram of a two-stage inverted pendulum.
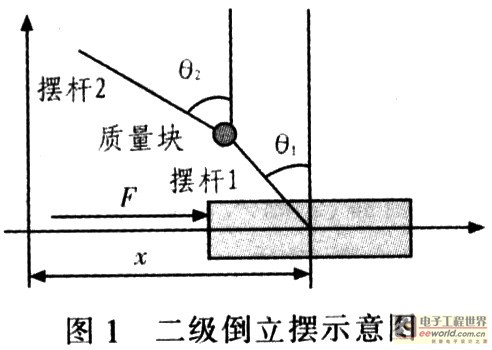
The parameters of the inverted pendulum are defined as follows: M is the mass of the trolley, 0.584 kg; m1 is the mass of the swing rod 1, 0.05 kg; m2 is the mass of the swing rod 2, 0.13 kg; kg; l1 is the distance from the center of the swing bar 1 to the rotation center, 0.077 5 m; l2 is the distance from the center of the swing bar 2 to the rotation center, 0.25 m; θ1 is the angle between the swing bar 1 and the vertical direction; θ2 is the angle between the swing rod 2 and the vertical direction; F is the external force acting on the system; g is the acceleration of gravity, 9.8 m / s2.
Use the Lagrangian equation to derive the kinematics equation. The Lagrangian equation is:
![]()
In the formula, L is the Lagrange operator, q is the generalized coordinates of the system, T is the kinetic energy of the system, and V is the potential energy of the system.

In the formula, i = 1, 2, 3 ..., n, fi is the external force of the system on the i-th generalized coordinate.
In the double inverted pendulum system, there are three generalized coordinates of the system, which are x, θ1, θ2. The state space equation of the system is obtained through calculation and linearization with human parameter values:
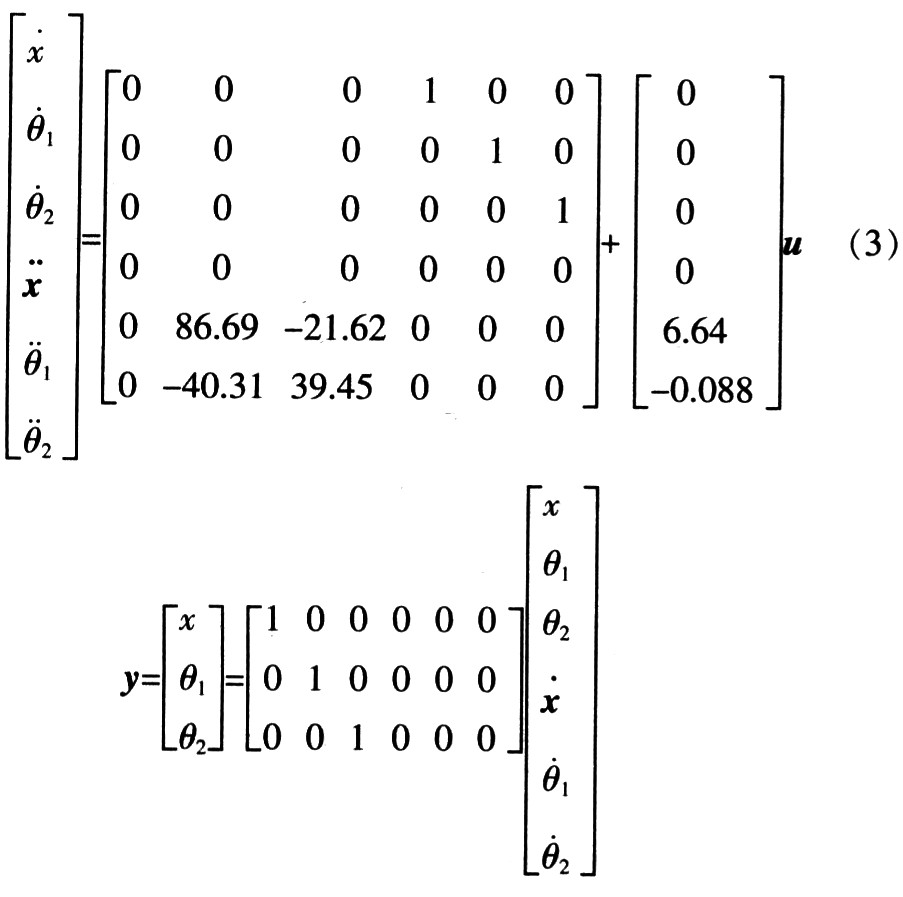
3 Design and simulation of two-stage inverted pendulum fuzzy control system
The secondary inverted pendulum system has many control targets, including the displacement of the cart, the swing angle of the lower swing, and the swing angle of the upper swing. The traditional fuzzy controller uses the system error and the derivative of the error as input. If the traditional fuzzy control is used to control the two-stage inverted pendulum, the fuzzy controller has 6 inputs: cart displacement, cart speed, sway angle, sway angle speed, upswing Swing angle and upswing angular speed.
If 5 fuzzy subsets are defined for each input variable, there are at most 56 control rules. The design of fuzzy control rules is complicated, and there are many adjustable parameters, which is not conducive to the complete formulation of fuzzy rules. This is the use of fuzzy control to study multi-variable non- The so-called "Rule Explosion" problem in linear systems. However, if three sets of two-dimensional fuzzy controllers (2 inputs and 1 output) are used to design the controllers in series or in parallel, the increase in the number of controllers greatly reduces the real-time control, and even out of control due to the inability to output the current control force in time .
3.1 Inverted pendulum control synthetic variable
This article is a fusion technique that combines optimal control theory with fuzzy control. It integrates the displacement, upper swing angle, and lower swing angle of the car into a variable E, and integrates the speed of the car, the angular velocity of the upper swing, and the angular speed of the lower swing into a variable EC, and E and EC are used as the input of the fuzzy controller. The voltage u is used as an output to reduce the input of the fuzzy controller and solve the problem of rule explosion, thus designing a Mamdani type fuzzy controller.
Through LQR simulation, input and output data pairs are obtained, and fuzzy rules are calculated and formulated based on the obtained data.
For the nested function Y = f2 [f1 (x)], first make f1 (x) perform preliminary processing on the input variables, and then use the algorithm f2 (x) to control according to the output of the previous algorithm. f1 is called the fusion function, and f2 is called the action function.
First use LQR in the optimal control theory to find the state feedback coefficient K and state vector x of the system:
![]()
In order to achieve variable fusion, two feedback coefficients are selected as control principal elements, and other input variables can be merged into the two principal elements according to the correlation and fusion with the principal elements. For the two-stage inverted pendulum, since the control difficulty of the pendulum rod 2 is the greatest, θ2 and θ2 are selected as the control principal elements, the corresponding coefficients are: kθ = kθ2, kθ = kθ2 The output vector of the fusion function is: 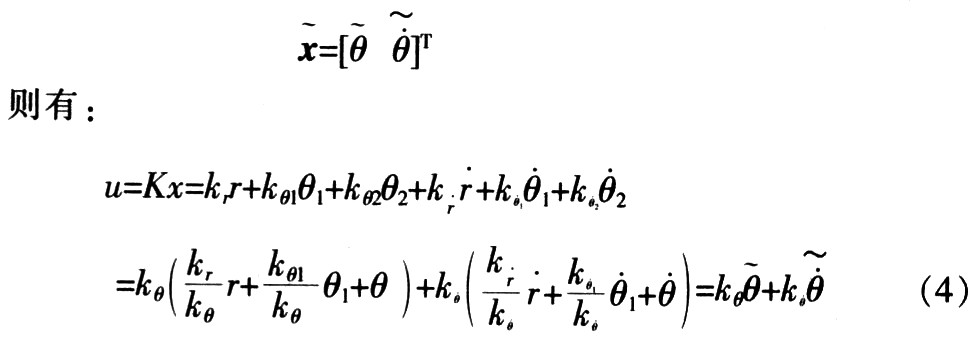
The output equation of the fusion function is:
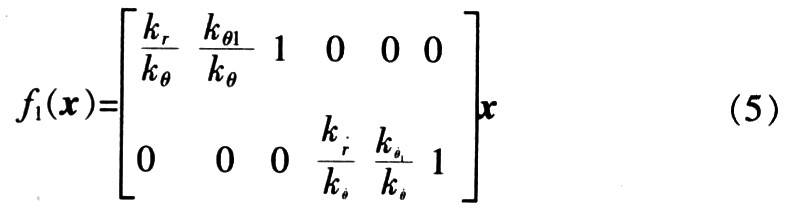
By reducing the dimensionality of the input state variables, the angular error E and angular velocity error EC are obtained:

Through information fusion, the six state variables of the system are converted into two state variables, which reduces the input of the system and realizes the dimensionality reduction of the fuzzy controller. Using the two variables E and EC obtained after dimensionality reduction as the input of the fuzzy controller, a two-dimensional Mamdani-type fuzzy controller is designed. Use optimal control to find K. The optimal control performance index function is:
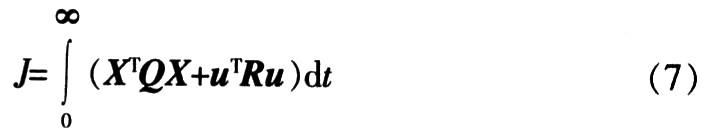
Minimizing equation (7), we can find:
![]()
Solve the following RicatTI equation to get the matrix P:
![]()
In the performance index function, the matrix Q and matrix R are defined to balance the sensitivity of the system to the input and state quantities. They have a great influence on the dynamic performance of closed-loop systems.
In the inverted pendulum system, Q and R are used to balance and weight the state vector x and the input control quantity u, respectively. In general, when P increases, the control force decreases, the angle change becomes smaller, and the following speed becomes slower. When an element in Q increases, the response speed of its corresponding state variable also increases, and the response speed of other state variables slows relatively. In order to make the feedback matrix K more reasonable, the selection of the matrix Q and R must be as appropriate as possible. Through repeated tests, the control process of the actual system selects Q = diag [500 700 700 0 0 0], R = 1.
According to the parameters of the second-level inverted pendulum, based on MATLAB's powerful matrix operation and its rich internal functions, the K = lqr (A, B, Q, R) command is used to calculate the state feedback matrix K:
![]()
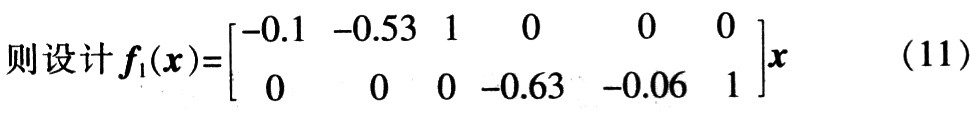
Thus, the comprehensive error E and the comprehensive error change rate EC are obtained.
3.2 Design two-dimensional Mamdani fuzzy controller after dimensionality reduction
Input variables E, EC, output variable u; E, EC domain setting: E ​​= [-6, 6], EC = [-6, 6], output domain U = [-1, 1] all use triangle Type, full overlap, uniformly distributed membership function. Each variable is described by five fuzzy subsets {NB NS ZE PS PB}, and the membership function curves are shown in Figure 2 and Figure 3. The membership function curve of EC is the same as that of E.
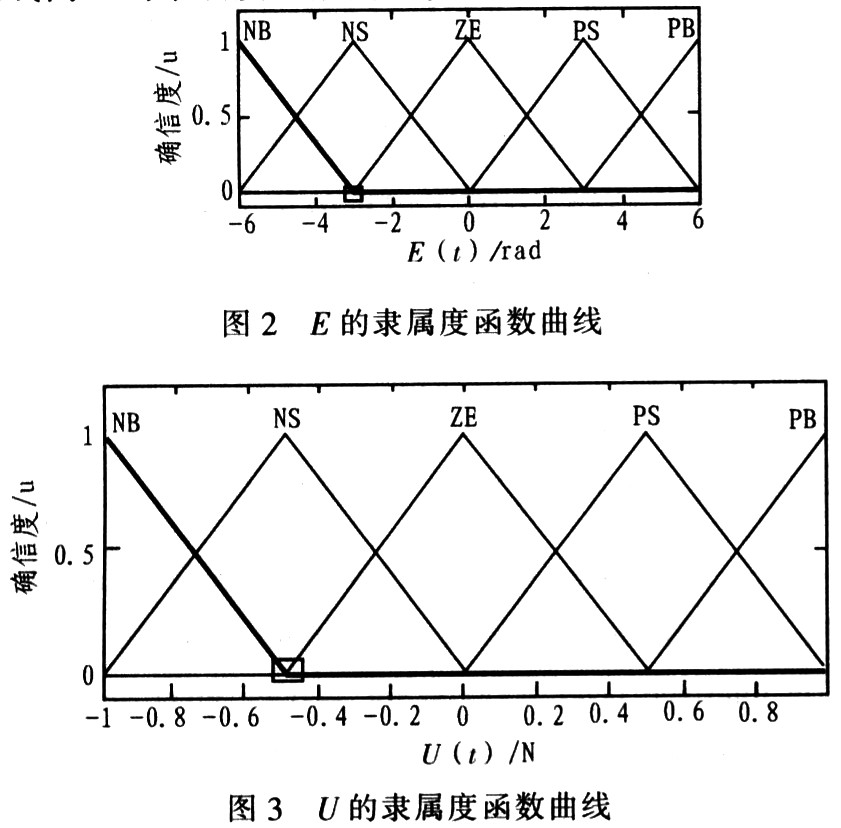
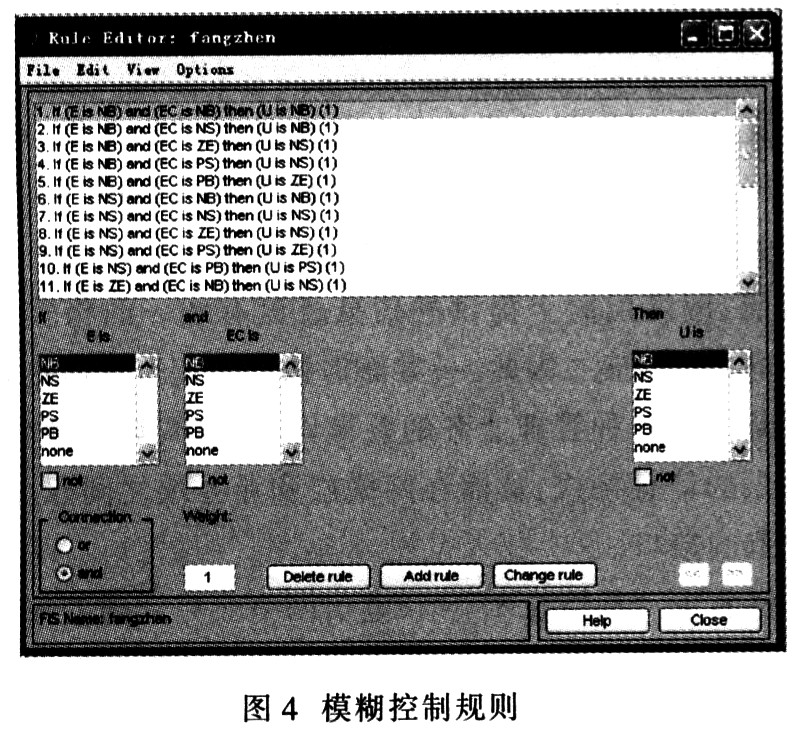
Fuzzy reasoning uses Mamdani's minimum calculation rules. According to the fuzzy linguistic variables on the input and output domains, NB (negative large), NS (negative small), ZE (zero), PS (positive small), PB (positive large) are designed. The fuzzy inference rules are designed as shown in Figure 4.
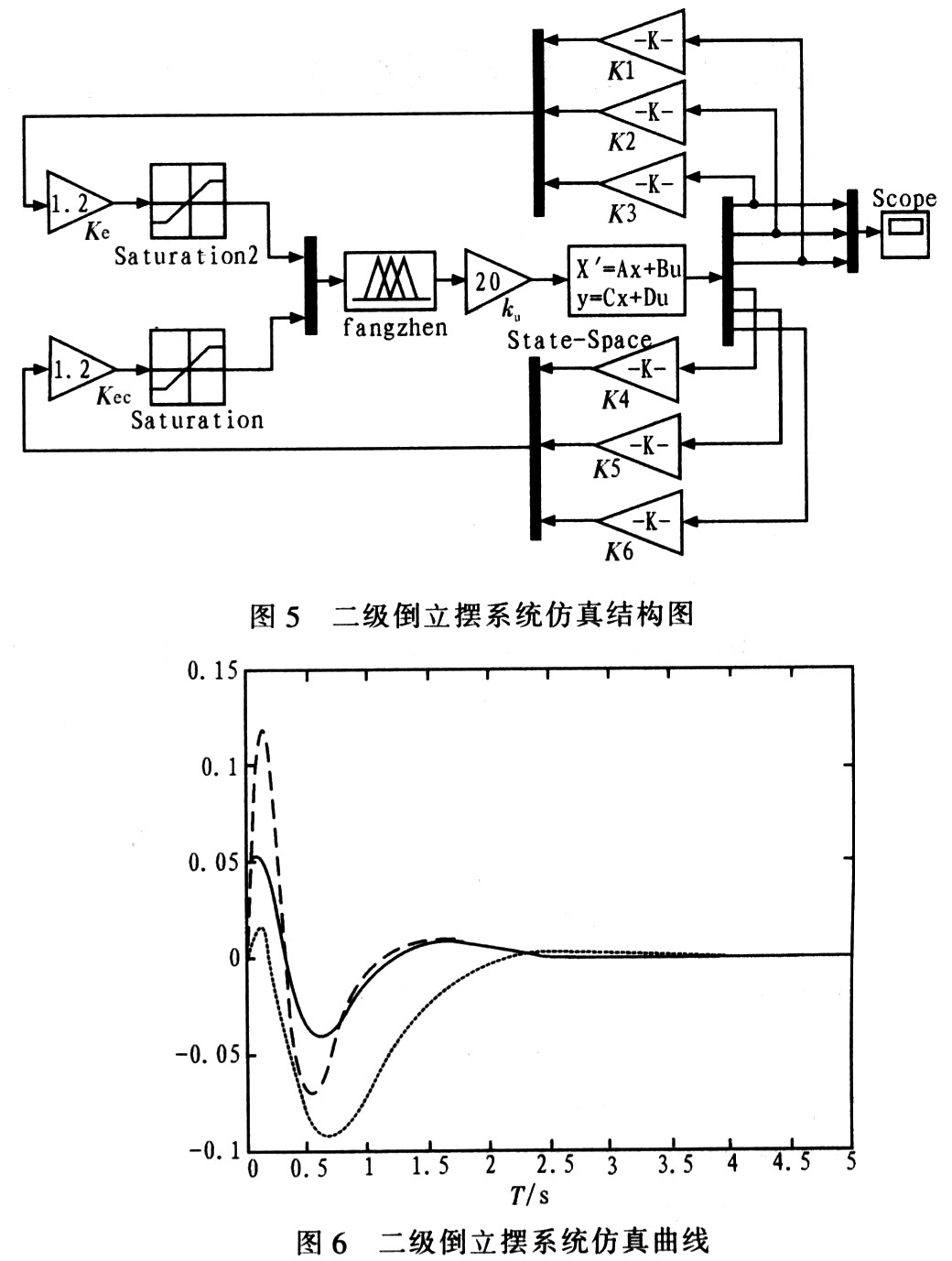
The fuzzy controller adopts the center of gravity method to achieve non-fuzzification. Compared with the general maximum membership method, the center of gravity method has smoother output reasoning control. Through the above analysis and experiment, and properly select the parameters of the fuzzy logic system, to design a fuzzy controller suitable for the controlled object, as shown in Figure 5. In Figure 5, Ke and Kec are quantization factors, Ku is a scale factor, State-Space is the state-space equation of the system, SaturaTIon is the limiting module, and Scope is the oscilloscope module. According to the above work, the second-level inverted pendulum system is simulated in the Simulink environment, and the simulation curve is shown in FIG. 6.
4 Conclusion
The double inverted pendulum is a typical multi-input, non-linear, strongly coupled system. By designing the fusion function to reduce the input dimension of the controller, and using fuzzy control to solve the problem of explosion of fuzzy rules encountered in multi-input systems, it becomes possible to design a practical fuzzy controller. The design method of fusion function can also be extended to the first- and third-level inverted pendulum systems. The design of the fuzzy controller is practical and feasible, which can control the system better and achieve better control effect. Fuzzy control has the characteristics of robustness, good stability, simple algorithm, etc. It is applied to the occasions with high real-time requirements, and the control method can also be applied to the control problems of other multivariable and nonlinear systems.
The Fume ULTRA is a pre-filled Disposable Vape pen device that is compact, a pocket-friendly size and easier to carry. Though the Fume Extra 1500 can vape 1500 puff. The Fume ULTRA Disposable Pen will last you longer with 2500 puffs and is powered by 1000mAh built-in battery and a huge 8ml pre-filled pod with tasty e-liquid. .
FUME ULTRA 2500puffs is a pre-filled disposable vaping device that is a pleasure to use. It has a circular light at the bottom of the pod that glows when inhaling the device. The Other product have 2500 puffs are Bang XXL Switch Duo 2500 puffs,Huge smoke Tugboat XXL 2500 Puffs,Slim stick AIVONO STICK 2500 Puffs, double flavor Bang Xxl Duo 2500 Puffs.
Device Details:
Size: 8ml
Nicotine Strength: 5.0%
Salt Nicotine equivalent to about 1 pack of cigarettes
Battery Capacity: 1000mAh
Puff Count: 2500+ Puffs
Flavors: 23 Available Flavors
Flavors:
- Raspberry Watermelon
- Strawberry
- Bubblegum
- Pina Colada
- Tangerine Ice
- Strawberry Watermelon
- Grape
- Pineapple Ice
- Strawberry Banana
- Strawberry Mango
- Pink Lemonade
- Cotton Candy
- Blue Razz
- Banana Ice
- Mint Ice
- Lush Ice
- Mango
- Melon Ice
- Rainbow Candy
- Cuban Tobacco
- Fresh Vanilla
- Purple Rain
- Blueberry Mint
- Tropical Fruit
Fume Ultra Disposable Vape, Fume vape kit,Fume Ultra Disposable Vape Pen,Vape 2500 Puffs
Shenzhen Essenvape Technology Co., Ltd. , https://www.essenvape.com